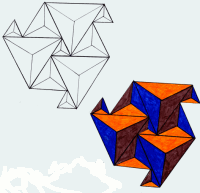
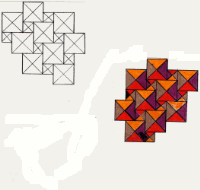
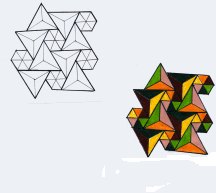
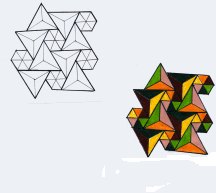
Generating patterns by introducing polygons in P3, P4 and P6.

Within the obliquity based lattice structures in P3 ,P4 and P6, repeat-units can be derived from a regular division of these lattice structures in polygons which mutually differ in lengthvalue.

repeatunit
in P3

repeatunit
in P4

repeatunit
in P6

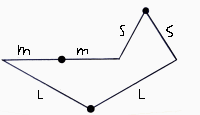
There are 3 values in the outlines of the repeatunits: S, M and L. The value M always equals L-S. In the repestunit, the values L, M and S are connected to the three types of rotationaxes we discriminate. In a stripe course, an M-event always occurs between two L-events. The S and |M values are exchangable. This means that in some cases the S-values are connecting the t2-fold rotationaxis in the outline of the repeatunit and in other cases the M/value. When the S/L-ration is greater than 1/2, the S-values are connecting the rotatationaxis; when the S/L-ration is smaller than 1/2 the M-values provide for tyhe connection.

Each level in the continued fraction has its own L, M and S values, as shown in the example beneath:

In each of the repeatunits the lattice-structure si divided in, we tolerate but one orientation of the line-motif. The results of this division of orientation of direction is thwe occurance of strip-courses or stripcircuits.
In each of the three symmetry types, the unit generates a stripecourse with a closed character , as shown beneath. In these examples, for P4 and P6 the length-units with a value M are not drawn in. They play no role in the ' steering' of the stripcourse, because the course traverses these lenght-units under right angles, thus not influencing the course of the strip. But to get fully grasp on patterngeneration, one should take acount of the M-values

Centre of the stripe-circuit

One of the three rotational axes lies in the centre of the strip-circuit, namely the axis that is connected to the value which is even. For every stripe-circuit per definition only one of the three values - S, L or M - is even. In the example beneath this regularity is illustrated in P6

L= sharp; S= obtuse

S=1
M=2
L=3

M-values connected to the 2-fold rotationaxis

S=1
M=1
L=2

L-values connected to the 6-fold rotationaxis

S=0
L=1
M=1

S-values connected to the 3-fold rotationaxis

Wonderfull stripe courses can be generated when the length values in the repeatunit become larger, as shown beneath for the p6-lattice:

q1=2
q2=1
q3=1
q4=1
q5=1
q6=5

q1=2
q2=1
q3=1
44=1
q5=7

q1=4
q2=3
q3=5

q1=2
q2=3
q3=5

Representing stripe-course by LS-series

The course of a strip is dependent on the indices of obliquity. The relation between the S/L-fraction and the strip course becomes clear if we if we apply the proces of continued fraction on this fraction, which results in a series of q-values.
In series of L/S-symbols there always are n or (n +1) L-symbols between two S-symbols. At the following levels the values n and 1 become symbols themselves; here too, the 'n -symbol' shows up alternately 'n or ('n+ 1) times between two '1-symbols'. At the last level, the number of occurrences of a "n-symbol" between two "1-symbols" is constant ( does not alternate between 'n and 'n+1). The relation between the continued fraction and this rewritten L/S-series, is now a matter of course: the number of chains in the continued fraction is equal to the number of strata in the L/S-series and the quotient of each link is equal to the value n of the regarding stratum. Application of this general model to the stratified spiralling structure which is generated by the fraction 5/17 in P6. There are three strata in this spiralling structure. The sixfold rotation axes are centra of spiralling at level I end level III; the two-fold axies at level II.

Hierarchically spiralling

The stripcircuit in essense has a hierarchical spirallingstructure. The three types of rotational axes can be involved at differend levels in this hierchically spiralling: In essence a strip-circuit (or, more accurately formulated, each of the symmetrical parts of its outline) always has the character of a stratified spiral . Simpler windings (lower strata) are included in more complex windings (higher strata), with more rotation axes involved in the total spiral winding pattern as stratification increases. In the example, 8 axes are involved: 1 red (fourfold) , 4 black (also four-fold) and three yellow (twofold), each at a specific level: the black at the lowest level, the yellow at the middle level and the red at the highest level.(Levels are marked with Roman numerals.). When the S/L is buided up in more than three layers, some are all rotationaxes are centre of spiralling at more than one level.

(For a clearing up in more detail the fenomenon of hierarchical spiralling click on the knob)

The structure of the spiralling is determining the the esthetic quality of the resulting pattern, so we must shed some more light on it.At every layer in the spiralling, the shape of the spiralling follows the shape of the stripe circuit at the level beforde. And concequently, the axes which is centre of spiralling, is the axis which lies in the centre of this l of that stripcircuit on the level before. The first layer hower is exceptional and we must spend some words extra on it.

The first level in the stripcircuit follows the shape of the stripcircuit indicated by the value L=1 and M=1 and S= 0 (Value S diminished to zero). In the case of p4 the shape of the spiralling at level 0 is in any case that of the square and in P3 that of the hexagon. In p6 it depends on the type of line unit the values L, M and S at higher levers lie on: Three options are possible: - if the L-values are connecting the 3-fold rotationaxis and the M-values the 2-fold axis, the shape at level 0 is that of the hexagon. - if the L-values are connecting the 6-fold rotationaxes and the M-values the 2-fold rotationaxes, the shape at level 0 is that of the trangle - if the L-value is connecting the 6-fold rotationaxes and the M-values the 3-fold axes, or the reverse, the shape at level 0 is that of the rhomb.

Example
In the example beneath , the utlimate stripecircuit is 13/69. There are three layers in the building up of the S/L-series:

q1=5
q2=3
q3=4

To make clear the buiding up of the spiralling structure we step by step build op the strip-course in its three layers:
As already stated, at every layer the stripecircuit,in its spiralling, follows the shape of the stipcircuit at th level before.

Hierarchically color-mixuring

Number of colors in symmetrical arrangement

(p.m.)

Hierarchically mixuring

The stratified property of a strip-course and the resulting strip-pattern can also find expression in stratified colour-clustering.

If more than two colours are introduced in a pattern, of which not all are involved in the spiralling action around a certain type of axis, colour-clustering may occur. In the example two patterns in p3 are shown: the number of strata in pattern a is two ; in pattern b four. At level II simple colour-clusering presents itself. At level IV an extra stratum in colour-clusteringshows up. The structure of the stratified colour-clustering at level IV is as follows: Both levels 'take place' around the same type of threefold rotation axis , which is involved at two levels in the spiralling- structure. At the higher level of involvement in this structure, the lower level in colour clustering takes place :

- colour 1 and colour 2 wind around each other;
- colour 1 and colour 3 wind around each other
- colour 2 and colour 3 wind around each other

At a lower level of involvement in this structure, the higher lever in colour clustering takes place. Now the three clusters (each composed of two colours) wind as a whole around each other:

- cluster (1+2) and cluster (1+3) wind around each other;
- cluster (1+2) and cluster (2+3) wind around each other;
- cluster (1+3) and cluster (2+3) wind around each other.

Reversion of sharp and obuse

In P6, for each strip circuit a complementary strip-circuit can be generated, in which the angles of 60 degrees are replaced by angles of 120 degrees and vice versa, as is shown by this overview of some simple fractions.The fraction remains the same, then, but the number of obtuse angles is linked to the other value in the fraction, and vice versa. So at one extremity of the value spectrum (number of obtuse angles zero) the triangle appears. At the other extremity (number of acute angles zero) the hexagon appears. In de middle of the value-spectrum (equal number of obtuse and acute angles ), only one strip-circuit exists, the diamond, that has no complement

Escher, too, had experimented with the possibility of reversion of the acute/obtuse ratio in strip-patterns, as appears from one of his notebooks.

In p4 and p6 there is - naturally - no reversion of sharp and obuse:

In decorational art through the ages there occur patterns inP3, P4 and P6which can be positioned within the summary tables

example in P3:

example in P4:

example in P6:

Swastica

The swastica in many versions appears as result of patterngeneration within direction based latice structures. It is regrettable that the Nazis in the past century has besmirched the symbol of the Swastica so much. It's a symbol deeply rooted in cultural expression of mankind . It was used by many cultures around the world, including in China, Japan, India, and southern Europe. The swastika symbolized life, sun, power, strength, and good luck, until the Nazis used this symbol to represent the darkest side of humanity. The picture at right shows a decoration with swasticas on a miedieval mosque, dating from far before the rise of the Nazism.

More variables in the repeatunit

More variables can be introduced in the repeatunit. The mathematical explanations of the patterns becomes more complex (less transparant) then, but richness in patternstructure decreases.Especially in P4 and P6.

The picture besides shows one way to introduce 4 length varables in the outline of the repatunit. But three are three other ways to connect them mutually in a angular way. Besides these different ormats in which theycan be connected, there are different ways to vary the lengthvalue of these lineunits. There must be some system in the way values are varied relative to each other:
- 2 by two 2 same value (in different versions)
- 1 by 3 the same value (in different version>
Of coures the number of variable lengthunits intruduces in a repatunit is unlimited. Further elucidation of this subject is presented onder the knob besides

(for more about more, click on the knob)

Intriguing color-mixures

Branching

OS-reversion quite complex

By the introduction of more variables in the area outline, it becomes possible to realize quite complex forms in the acute/obtuse-reversion, related to the symmetry of the strip-circuits which are generated by these variables, as this overall picture of some simple examples, based on the area-outline presented in fig. 10a, shows: - For some fractions the reversion takes place in one and the same strip-circuit. In these cases, in certain parts of the strip-circuit the pattern of acute/obtuse alternation is the reverse of that in other parts. Nice examples may be found at the one extremity and in the middle of the value-spectrum: the diamond and the trapezium. The first is symmetrical and consists of four parts two of which (in opposite positions) are equal and the reverse of the other two.This causes the sequence acute, obtuse, acute , obtuse, that is typical for the diamond. The last is asymetric and consists of two parts which are the reverse of each other : the acute/obtuse sequence in the one part is followed by the obtuse/acute sequence in the other part, which causes the trapezium-like outline of this strip-circuit. - For other fractions two different circuits occur in a pattern. In the one, the obtuse angles come in the place of the acute angles in the other, and vice versa. The combination of hexagon and triangle is a nice example, in the other extremity of the value-spectrum.

Working with stripy patterns which already exist in decorationart.

It can be challenging to create variations on stripy patterns which are the heritage of old cultures.Which patterns are qualified for that aim? We first describe the type of stripy pattern which are qualified. Next we show hown to introduce lengthvariables within such patternsFinally we treat the princple of continued subtraction, which besides the principle of continued fraction can give some insigh in the relation lenth-values and stipe-course characteristics

Definition of stripy patterns

Introducing lines of deflection within stripy patterns

The principle of continued subtraction

Centre of the stripe-circuit One of the three rotational axes lies in the centre of the strip-circuit, namely the axis that is connected to the value which is even. For every stripe-circuit per definition only one of the three values - S, L or M - is even. In the example beneath this regularity is illustrated in P6 L= sharp; S= obtuse
	S=1 M=2 L=3 M-values connected to the 2-fold rotationaxis
	S=1 M=1 L=2 L-values connected to the 6-fold rotationaxis
	S=0 L=1 M=1 S-values connected to the 3-fold rotationaxis

Wonderfull stripe courses can be generated when the length values in the repeatunit become larger, as shown beneath for the p6-lattice:
	q1=2 q2=1 q3=1 q4=1 q5=1 q6=5	q1=2 q2=1 q3=1 44=1 q5=7
	q1=4 q2=3 q3=5	q1=2 q2=3 q3=5

The course of a strip is dependent on the indices of obliquity. The relation between the S/L-fraction and the strip course becomes clear if we if we apply the proces of continued fraction on this fraction, which results in a series of q-values.
	In series of L/S-symbols there always are n or (n +1) L-symbols between two S-symbols. At the following levels the values n and 1 become symbols themselves; here too, the 'n -symbol' shows up alternately 'n or ('n+ 1) times between two '1-symbols'. At the last level, the number of occurrences of a "n-symbol" between two "1-symbols" is constant ( does not alternate between 'n and 'n+1). The relation between the continued fraction and this rewritten L/S-series, is now a matter of course: the number of chains in the continued fraction is equal to the number of strata in the L/S-series and the quotient of each link is equal to the value n of the regarding stratum. Application of this general model to the stratified spiralling structure which is generated by the fraction 5/17 in P6. There are three strata in this spiralling structure. The sixfold rotation axes are centra of spiralling at level I end level III; the two-fold axies at level II.

The structure of the spiralling is determining the the esthetic quality of the resulting pattern, so we must shed some more light on it.At every layer in the spiralling, the shape of the spiralling follows the shape of the stripe circuit at the level beforde. And concequently, the axes which is centre of spiralling, is the axis which lies in the centre of this l of that stripcircuit on the level before. The first layer hower is exceptional and we must spend some words extra on it.
The first level in the stripcircuit follows the shape of the stripcircuit indicated by the value L=1 and M=1 and S= 0 (Value S diminished to zero). In the case of p4 the shape of the spiralling at level 0 is in any case that of the square and in P3 that of the hexagon. In p6 it depends on the type of line unit the values L, M and S at higher levers lie on: Three options are possible: - if the L-values are connecting the 3-fold rotationaxis and the M-values the 2-fold axis, the shape at level 0 is that of the hexagon. - if the L-values are connecting the 6-fold rotationaxes and the M-values the 2-fold rotationaxes, the shape at level 0 is that of the trangle - if the L-value is connecting the 6-fold rotationaxes and the M-values the 3-fold axes, or the reverse, the shape at level 0 is that of the rhomb.

Example In the example beneath , the utlimate stripecircuit is 13/69. There are three layers in the building up of the S/L-series: q1=5 q2=3 q3=4 To make clear the buiding up of the spiralling structure we step by step build op the strip-course in its three layers: As already stated, at every layer the stripecircuit,in its spiralling, follows the shape of the stipcircuit at th level before.

The stratified property of a strip-course and the resulting strip-pattern can also find expression in stratified colour-clustering.

If more than two colours are introduced in a pattern, of which not all are involved in the spiralling action around a certain type of axis, colour-clustering may occur. In the example two patterns in p3 are shown: the number of strata in pattern a is two ; in pattern b four. At level II simple colour-clusering presents itself. At level IV an extra stratum in colour-clusteringshows up. The structure of the stratified colour-clustering at level IV is as follows: Both levels 'take place' around the same type of threefold rotation axis , which is involved at two levels in the spiralling- structure. At the higher level of involvement in this structure, the lower level in colour clustering takes place : - colour 1 and colour 2 wind around each other; - colour 1 and colour 3 wind around each other - colour 2 and colour 3 wind around each other At a lower level of involvement in this structure, the higher lever in colour clustering takes place. Now the three clusters (each composed of two colours) wind as a whole around each other: - cluster (1+2) and cluster (1+3) wind around each other; - cluster (1+2) and cluster (2+3) wind around each other; - cluster (1+3) and cluster (2+3) wind around each other.

	In P6, for each strip circuit a complementary strip-circuit can be generated, in which the angles of 60 degrees are replaced by angles of 120 degrees and vice versa, as is shown by this overview of some simple fractions.The fraction remains the same, then, but the number of obtuse angles is linked to the other value in the fraction, and vice versa. So at one extremity of the value spectrum (number of obtuse angles zero) the triangle appears. At the other extremity (number of acute angles zero) the hexagon appears. In de middle of the value-spectrum (equal number of obtuse and acute angles ), only one strip-circuit exists, the diamond, that has no complement
	Escher, too, had experimented with the possibility of reversion of the acute/obtuse ratio in strip-patterns, as appears from one of his notebooks.
In p4 and p6 there is - naturally - no reversion of sharp and obuse:

In decorational art through the ages there occur patterns inP3, P4 and P6which can be positioned within the summary tables

More variables in the repeatunit More variables can be introduced in the repeatunit. The mathematical explanations of the patterns becomes more complex (less transparant) then, but richness in patternstructure decreases.Especially in P4 and P6.
	The picture besides shows one way to introduce 4 length varables in the outline of the repatunit. But three are three other ways to connect them mutually in a angular way. Besides these different ormats in which theycan be connected, there are different ways to vary the lengthvalue of these lineunits. There must be some system in the way values are varied relative to each other: - 2 by two 2 same value (in different versions) - 1 by 3 the same value (in different version> Of coures the number of variable lengthunits intruduces in a repatunit is unlimited. Further elucidation of this subject is presented onder the knob besides	(for more about more, click on the knob)