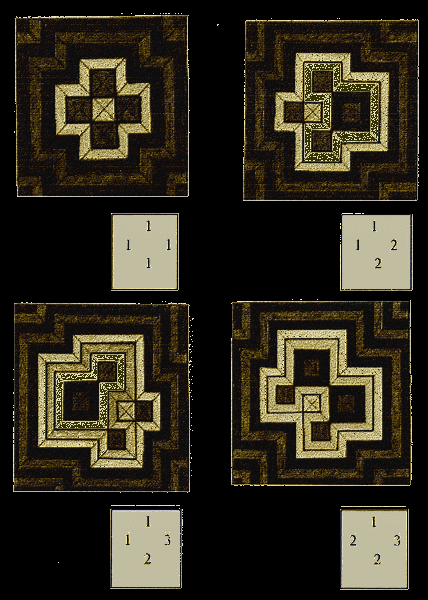
The principle of continued Subtraction

In successive steps, certain values (s) are subtracted from the original values in the scheme, until all rest-values have reached zero. To determine these values (substrahends), in each step specific zones are selected from the overall value-scheme. In each of these zones, the lowest value is the subtrahend s . It is subtracted from all values in that zone. So in each zone at least one value reaches the level zero. The value of the subtrahend is equal to the number of strip-circuits that arises as a result of this part of the continued subtraction. The shape of the circuits which arise as a result of the subtractions in a certain step are specific for that step. It is related to the attributes of the zones selected in that step. Circuits that arise in later steps encompass circuits that arise in former steps.