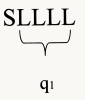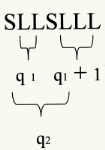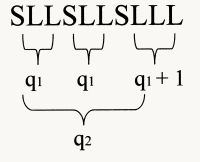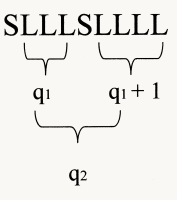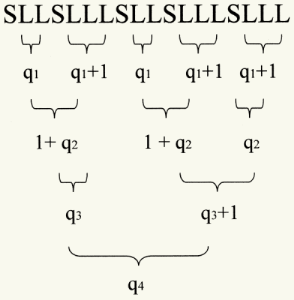Generating patterns by introducing obliquity
Content
1 Introducing obliquity
2 Lattice structures based on obliquity
3 Crossing-up of the cross
4 Cutting-up of the honeycomb
1. Introducing obliquity in plane-symmetries
Miller indices
Abbe Huay who was the founder of crystallography had been the first to presume that crystal faces
often held a slanting position in relation to the pattern in which the building stones of the crystals
involved were arranged and that this obliquity could be expressed in simple integers. Though his
presumptions were correct, he was not able to clarify them in a way which could withstand the test of time.

As insight in crystallography matured, it was a Professor of Mineralogy at the University of Cambridge,
W.H.Miller, who - in the course of the 19th century, and profiting from the new insights in this matter -
developed a useful system for the indexing of this obliquity of crystal faces by means of simple ratios.
The integers in these ratios are called 'Miller Indices'.
Miller started from the concept of repeat-units, as was traditional in crystallography. The various types
of plane-symmetry are considered to be built up of repeat units which always have the shape of parallelograms.
Starting from this viewpoint, the indices of obliquity are equal to the number of times in which the vertical
and the horizontal sides of the repeat unit are traversed by crystalfaces.
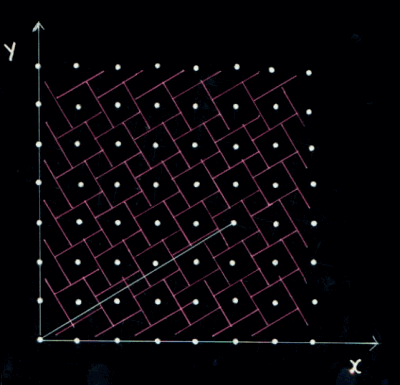
SL-series
Walking in de direction 2/5 generates the sequence SLLSLLL.
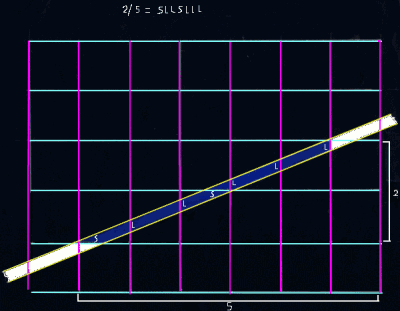
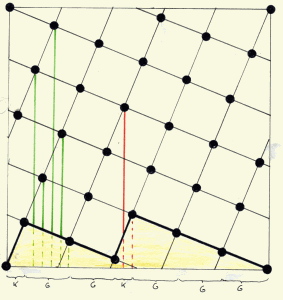
| The obliquiy in the example (besides) is reprsented
by the fration 2/5. That means that seven events occur in cetrain succession and againand aguin in that succession
while walking over the stroke-path: 5 L-events (=crossing a purple line)
and 2 S-events (=crossing a green line).After seven events, the pattern is repeated The way in which the L- and S-events alternate is in principle hierarchically layered.
The relation between this hierarchically layeredness and the fraction indicative of the obliquity can be made transparant
by representing the fraction as a continued fraction. |
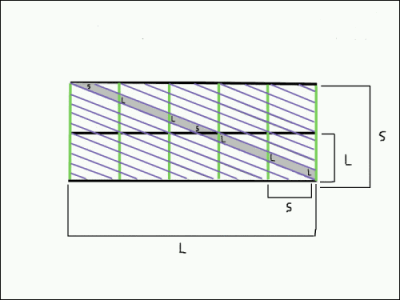
| Because we need to obey to the rules of symmetry,
the in obliquedirection running stroke schould be repeated in a regular way. It intersects the puple sides
of the repeatunts L +=5) times and the green sides S+=2) times.So the obliquity is also represented by this intersectio-ratio (indices of Miller)
of these sides. |

| The effect of obliquity can be transformed in some sense
by introducing repeateunits of differents size.Now the events which are generated bij walking over a stroke-path
are crossing a large (L) and crossing a small(S) repeatunit. The pattern of alternation of L- en S events remains the same.
|
|

| We can represent
the obliquity by a line instead of by a stroke. The 7 events start and end at a corner of a repaetunit.
When we decide that the event at the startingpoint is a S-event, that at the endingpoint musty be a L-event. Such a sequence of seven events , generated by the line while running through the plane,
can be conceived as the 'motif' of the plane-symmetry.
the endingpoint is a Levent. |
| Here too, the efefct of obliquty cn be transformed by introducing repeatunitsof different sizer. |
Algorithme
Every direction (obliquity relative to arrangement of repeatunits) though a plane-symmetry,
represented by an unique fraction, generates an unique sl-series:
1 Let y = L
2 For n= 1 to L
3 Let y = y + S
4 If y > L then let y = y - L : Print S
5 Print L
6 Next n
Continued fraction
The way the structure of the SL-serties is related to the fraction which represents the direction in the plane-symmetry seems
ondoorgrondelijk but becomes volstrekt clear if we rewrite the fraction as a continued fraction. Let us explian how that is done.
However before we need to
explain the continued fraction
Every fraction can be represented by a number of quotients (q1, q2, q3,.. ),resulting from a process of
successive divisions. To begin with, the denominator of the fraction is divided by its numerator (divisor);
then the divisor of that first division by its rest, etcetera, untill the rest is zero. This 'decomposition'
of the fraction can represented as a continued fraction or 'Kettenbrüche'. In the example the fraction 103/356,
this fraction can be 'decomposed' in the following series of q(uotient)-values: q1=3; q2=2; q3=5; q4=4; q5=2.
Written in the notation of a 'Kettenbrüche':
103/356 = 1
3 + 1
2 + 1
5 + 1
4 + 1
2
On internetther can be fond a site onwhich for every fration the continued fraction is represented in this notation-systematiek. enz.
Relation between the sl-series and the continued fraction
In series of L/S-symbols there always are n or n+1 'L'-symbols between two 'S'-symbols.
At the following levels the values n and 1 become symbols themselves; here too, a 'n'-symbol
shows up alternately n or n+1 times between two '1'-symbols. Ecetera. At the last level, the number
of occurrences of a 'n'-symbol between two '1'-symbols is constant (does not alternate between n and n+1)
and equals n at this level.The relation between the continued fraction and this rewritten L/S-series, is
now a matter of course: the number of chains in the continued fraction is equal to the number of strata
in the L/S-series and the quotient of each link is equal to the value n of the regarding stratum.
In the following some examples. First some examples of series with one strata, then onee
with two stata, then some with three and finally one with four strata.
|
|
examples of Sl-series with one stratum
|
 |
1/2
q-values:
q1=2
|
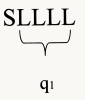
|
1/4
q-values:
q1=4
|
|
examples of Sl-series with two strata
|
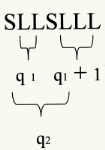
|
2/5
q-values:
q1 = 2
q2 = 2
|
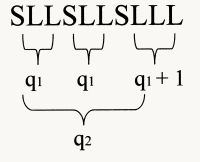
|
3/7
q-values:
q1 = 2
q2 = 3
|
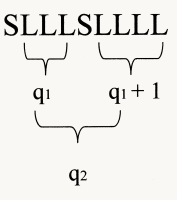
|
2/7
q-values:
q1 = 3
q2 = 2
|
|
example of Sl-series with three strata
|
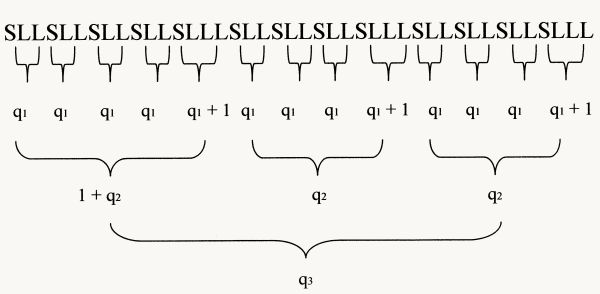
|
13/29
q-values:
q1 = 2
q2 = 4
q3 = 3
|
|
example of Sl-series with four strata
|
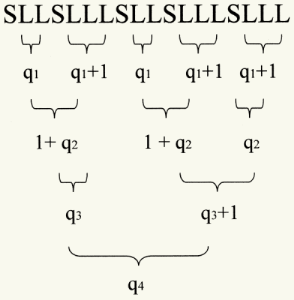
|
5/13
q-values:
q1 = 2
q2 = 1
q3 = 1
q4 = 2
|
"q" or of "q+1" dominant
|
As may become clear from the preceding tabel, every stratum in a SL-series can be conceived as builded up out
of "q" and "q+1" elements. One of the two is dominant at a certain stratum. As the next q value is 1,
at the stratun belonging to the precweding q-value, q+1 is dominant.If that value is greater than 2,
de "q"-element at the preceding stratum is dominant. If that value is 2 , nor the element "q" nor the elemant "q+1"
is dominat. In this case theren is but one "q"-elemnt and one "q+1" elemant at tha preceding statum. So the value 2 has specific meaning, in the sense that the belong stratum represents
exeptions.
At the last strutom there is no "next q-value. this stratum consists of only one "q-element.
|
Different form the concept of Miller indices
When the first q-value in the continued fraction is one, the enumerator in the
fraction is more than half the value of the numerator. In those cases we can conceive the builing up if the series as
the number of times lm-elements are alternated by a ls-element. In these cases the lm -element occurs n or n-1 times
between two LS- elements. The value s in these cases is represented by the diagonal line in the repatunits, which itself als can be cinceived as onde of the outlines of a larger repeatunit.
In these cases,
is one, n+1 is dominant in de SL-series at the different layers
2. Lattice structures based on obliquity
The 17 plane-symmetry-groups
|
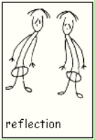
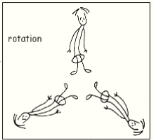
There are 17 types of plane-symmetries or wallpaper-groups. Each is composed in specific way out of one or more of four types of "spatial
transformation: shift, rotation, reflection and slide-reflection:
|
|

|
So the seventeen can be classified in terms of the occurence of these four types of spacial transformation.
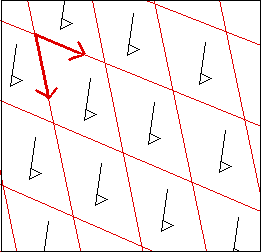
The most simple type is that in which occur shifts only.
At the base of this type pattern lies the regular repetition of the shift, which makes that the pattern can
be grasped as a tacking together of parallellograms, each of which can be seen as the "repeat-unit" containing
all the information about the complexity of the pattern.
|
|
The shiftpattern and the 'repeatunits' which are generated by it, also lie at the
base of the remaining sixteen types of symmetry. But these sixteen contain other 'symmetrical
operators' besides the shift, which makes there structure more complex (independant of
the characteristics of the motif used).
The following table presents the characteristics of the other sixteen types of plane-symmetry.
|
(Click on the type-indications.)
|
|
type |
highest rotation |
reflection |
glide-reflection
|
|
pg |
1 |
no |
yes |
|
pm |
1 |
yes |
no |
|
cm |
1 |
yes |
yes |
|
p2 |
2 |
no |
no |
|
pgg |
2 |
no |
yes |
|
pmg |
2 |
yes |
yes |
|
pmm |
1 |
yes |
no |
|
cmm |
2 |
yes |
yes |
|
p3 |
3 |
no |
no |
|
p31m |
3 |
yes |
yes |
|
p3m1 |
3 |
yes |
yes |
|
p4 |
4 |
no |
no |
|
p4g |
4 |
yes |
yes |
|
p4m |
4 |
yes |
yes |
|
p6 |
6 |
no |
no |
|
p6m |
6 |
yes |
yes |
|
|



|
In p3 there occur 3 types of 3-fold rotational axes.
In p4 there occur 2 types of 4-fold rotational axes and 1 type of 2-fold rotational axes (the last in 2 orientations in space).
In P6 there occur 1 type of 6-fold axes, 2 types of 3-fold axes (in 2 orientions in space) and 1 type of 2-fold axes (in 3 orientations in space)
Escher realised beautiful expressions within these arrangements
|



|
the numer of oriemtations in pace of a motif
The number of orientations in space of the motif differs in each of these three
symmetry types groups and equals the highest 'foldness' of rotationaxes which occur there. In p6, motifs have
six different orientations in space; in p4 four different orientations and in pr 3 different oreintations and in p2 two
different orientations.
|
Lattice-structures in P3, P4 and P6
Let 's go back our idee of a direction in the symmetrical universe, generating a S/L-series. Until now we
illustrated this fenomenon as if it concerns symmetry structures in which only shifts are occurring.
But direction-related SL-series can also occur inmore complex plane symmetries in which other symmetry elements occur besides the shift.
In such symmetries, directions ' run' in different orientatations
which results in quite intriguing interatios between SL-series.
Especially in symmetries in which rotation axes occur besides shifts, generating S/L-series can result
in quite intriguing patterns.
Before we shed some light on this, we should spend some attention the concept of direction within these types of symmetry. In these types of symmetry the concept of direction is complicated and we shoud first shed some light on it.
what 's meant by the concept of "direction" in P3, P4 and P6?
The word "direction" in first instance indicates the degree of obliquity relative to the repeatunits which
represent the regular shiftpattern which in every case underlies a planesymmetry (wallpapergroup).
But dependent on the occurence of other element of symmetry (rotations, reflections, slide-reflections),
a "direction" besides a degree of obliquity can possess different orientations in space.
In those cases a direction is defined by its degree of obliquity and its orientation in space |
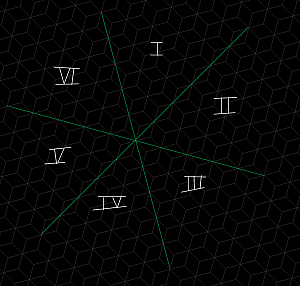 | 6 orientations
in space |
|
 |
obliquity = 2/5
orientation = II
| |
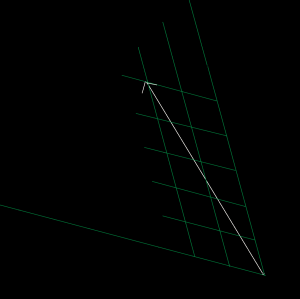 |
obliquity = 2/5
orientation = IV
|
The values 2 and 5 on the coordinates, for each orentation of course can be reversed. As long as
there occur no reflections besides rotation in, the way the valyes are positioned needs to be consistent in
the sense that it must be in accordance with the rotationsymmetry in question.
|
line-motif
It is convenient to conceive the line representing the direction, marked out by
two(highst foldness) rotationaxes
as the "motif" (line-motif). On a mitif-line a number of events occurs, walking from the roationaxis at the 'departure' to the rotationaxis a the 'arrivel'
|
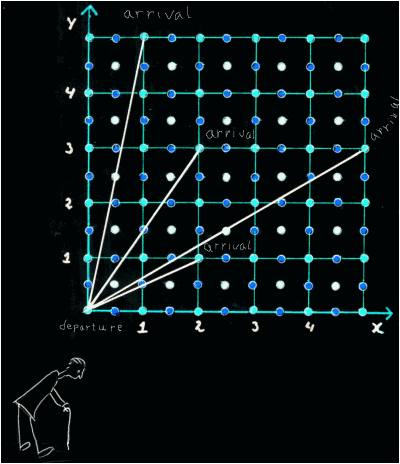
|
|
|
lattice structures generated by direction
Chosing a direction (line-motif) in P3, P4 or P6, this direction automatically occurs in four
different orientations.The result is acomplex lattice-structure. To onderstand how patterns can be generated out of the laticestructures, i
we need to shed som light on the structure of these lattiices. There are two important characteristics:, which both can be conceived at the level of the line-motif:
1) the pattern of shifts in the way a linemotif is traversed by line-motifs runningin other orientations
2) the pattern in the scatterin of sets of identical points on the line-motif. Beneth, these characteristics are elucidated for P4.
Under the knob at the right, a closer look is offered at these characteristics in P3 and P6. |


 |

For elucidation of
characteristices
in P3
and P6 click on the knop
|
pattern of shifts in the intersectionstructure
|
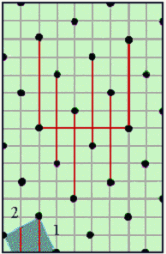
|
Every line-motif is intersected by other line-motifs at regular distances (one or two lin-emotifs intersect
at ech point, depending on the symmetry type ). This results in a pattern of
upward and downward jumps.
|
The buiding up of this shift-pattern is explained in more detail under the knob at the right |

(click on the knop) |
The smalles distance we conceive as the unit of distance.
The traversing line-motifs show shifts in their position relative to each other. This pattern of shifts in the traversing line-motifs
can be represented by a series of symbols u (upward shift) and d (downward shift).
In p6 and P4 each line-motif inheres two orientations.
On such lines at the midpoint there is reversion in the succession of SL-events,related to reversion of
what's at left and at right.
|
|
|
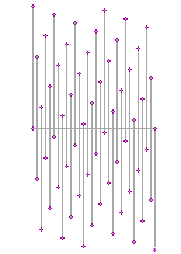
|
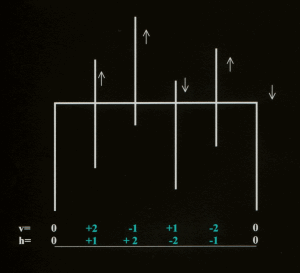
The complexity of the u/d-series can be derived
from the ratio between the shiftdistances of the u-shifts and the d-shifts.
These distances can be calculated on base of the following two formula's:
(1) ax +by= + 1
(2) s=bx+ay
where x and y are the values in the ratio for obliquity.
In the example besides s(d)/s(u)=12/17. When we represent this fraction as a continued fraction (series of q-values),
the relation between the structureof the u/d-series and the indices for obliquity become clear.
|
 |
Relation between S/L-series and U/D-series
The structure of the U/D-series resembles that of the S/L-series
The series of q-values representing the U/D-series, is composed of two times the series
of q-valoues representing the S/L-series, with a point of reversal half way.
But the first q-value within the total series of q-values always has to be
diminished with 1 (see examples).
The picture beneath explains this reversal in the q-value-series.
|
The fraction for obliquity = 2/5. There are two
levels in the corresponding S/L-series and within each, half of the pattern of the U/D is generateed in such way
that de SL-series and UD series match. |
 |
| Example 2/7, | | obliquity
2/7 | S/L = 2/7
q-series:
q1 = 3
q2 = 2
| U/D=23/30
q-series:
q1 = 2
(-1)
q2 = 3
q3 = 3
q4 = 2
|
|
Example 4/11 |
obliquity
4/11 | S/L = 4/11
q-series:
q1 = 2
q2 = 1
q3 = 3
| U/D=37/100
q-series:
q1 = 3
(-1)
q2 = 1
q3 = 2
q4 = 2
q5 = 1
q6 = 3 |
|
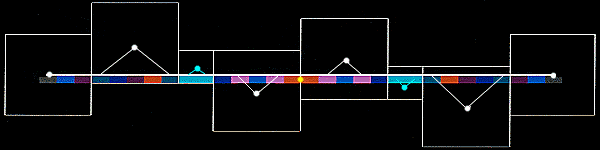
Pattern in the scattering of sets of identical points on the line-motief
The intersectonpoints of a line with lines running in other direction results in a scattering pattern of identical
point (points which are equal in isometrical sense but different qua orientation in de the space.
In the elucidation of this aspect, we focus on P4. The number of identical points in a set of identical
points equals the number of orientations in the symmetry type. In the explanation we focus on P4. Withing this symmetry type
each set of identival points consists of four points. As stated before,in P4 on each linemotif two otientations of direction are integrated,
so there is a reversion around the midpoint on the line. So, of each set of identival poing tw lie at the onde side and two lie at the other side of the midpoint.
In de example beneath first this is eludcidateed for obliquity 1/2. In this case there is, besides the rotationalaxes which form the beginning and the end of the line-motif . Inbetween
there is but one set of identical points, of which twe are positioned at the left side and two at the right side of the midpoint.
|
| S/L= 1/2.
In the picture at the left the SL-ratio is 1/2 there occurs but one set of 4 identical points between the rotation axes at the extrimities.
In the picture beneath, the S/L-ratio is 2/5. In this example there occur 7 sets of identical points (each sert marked with a different color)between the rotationaes at the extrimities.
In this example also the U/D-shiftpattern is belongen to this obliquity is represented.
|

|
The way the sets of identical point are scattered over the line is complex.
This complexity can best be understand by laying a template on the latticestructure deviding it in polygons of different size.
|
 |
 |
 |
If we take the example above of the scattering pattern belonging to obliquity 2/5,
laying a template of polygons on the latticestructure
makes this pattern transparant to some degree, as is shown in the picture beneath. Pairs of identical points within the greater polygons alternate with pairs
of identical points within the smaller polygons.The pairs of identical points derive there mutually equality from the (4-fold) rotationaxes lying in the centre of the polygons
(and , as far as concens the pair of identical points in the centre, from the 2-flod axes positioned there). So, the scatteringpattern of these pairs is directly related the the pattern of alternation
of the two types of 4-fold rotationaxes . This pattern is directly related to the S/L-fraction, decomposed as a continued fraction.
|
Regular planedivision by polygons has a long tradition in decoration art. Famous pattern is that originating form antique Babylonie,
which Owen Jones
Owen jones describes in his GRammar of Ornaments |
 |
Two approaches for patterngeneration
The characteristics of the lattice structures we spoke above are
startingpoint for two different approaches in patterngeneration:
- patterngeneration on ground of the scatteringpattern of pairs of identical points
In this approach, we follow the scattering pattern of pairs of identical point . Succesively, there are pairs of points which are not identical, alternated by pairs of points that are identical.
The linesegmentes lying between paires of identival points are not drawn in.
The approach is explained under Euler-knob 3.
- patterngeneration on ground of 'dotted' lines
In this approach, we simply make a 'dotted' line of the linemotif.
We successively draw a line between a pair of intersectionpoints and pass over the next pair.
This approach results in cristallike figures. The approach is explained under Euler-knob 4
|
patterngeneration on ground of the complexity of
the pattern in scattering of sets of identical sets.

S/L=2/5
| |
pattern generation on ground of dotted lines

S/L=2/5 |
3. Crossing-up of crosses.
I Mathmatical rules
In this approach of generatiing patterns out of obliquity based lattice-structures, the motif is a line-segment between 2 rotation axes. Such a line is intersected many times
by line-segments running in an other orientation. So the line is diveded in lots of equal pieces. Of these ,
we successively draw one and pass over the next .
The result are cristal like figures, the shape of which depends on the obliquity of the line-motif (S/L-ratio.)
In the scheme beneath, some basic elements of these figures are elucidated in relation to the series of q-vaqlues which represent
the S/L-series as indication of the obliquity. |
.

  |
At the left the basic elements in buiding up of cristalline patterns are presented:
squares and 'notched' lines. In the categorie of noched elements we discriminate z-wise-notching and
u-wise-notching. The occurence isrelated to the u/d ratio (explanation u/d-ratio under Euler-knob2.
The relative frequency of occurense of thsee three elements in a cristalline pattern and the types of combinations
between them, is directly related tot the u/d-ratio. |
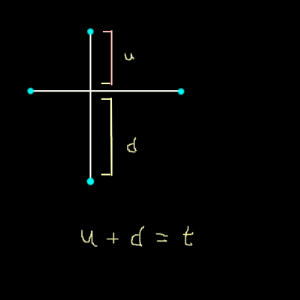
|
To elucidate this
relation we first must focus for a while on the u/d-ratio itself. Togethe these values represent
the total number of line-units on a line motif . We call that total numer T. So U + D = T). The value t always must be uneven,
otherwise the line-motif has a fourfold rotation axis in the mid. And in that case we are taking of two linemotifs with each T/2 line units.
So in every case the value u must be even and the value d uneven, or the reverse.
|
|
|
|
| For understanding the structures which are genereated , it is conceniant two look
how pairs of linemotifs running in one orientation intersect with pairs of lines running in the other orientation
In the position of pairs of line-motifs running in one one orientation are two options: the segments which are drawn lie on the same level
or they lie or the differ one unit of distance. But the can only have that position to same extent, because there is a shift-relation between them. So the position shifts after a distanc of u.
The same applies to pairs of lines running in the other orientation.
If the valu D (largest disctance is even and value U (smallest disctance is uneven,
the main pattern is that of a zigzag-wise nothching, resulting fron intersection of pairs of lines which have
unequal levels of drawing in line-segments.
In the same sense, when the value U is ebven and D is uneven, the sguares dominate in the pattern
In both cases, some of the interactions between pairs results in a u-wise notching, resulting from an intersection in whihich a pair of lines in one orientation is equal levveled and in the othor direc tion is un equal levelled.
But the elemnts are never dominant and are connected to te S-value in the S/L-fraction.
|
|
|
The different level combination within pairs of line-motifs at different levels in the U/D-series can occur and cause combinations in combinations which were created at the level beforefore
When the u value at a certain leven is even, at the next level the genereated combinations are like
shown in figure a).
When the u value at a certain leven is uneven, at the next level in which the u-value occurs,
the generated combinations are like shown in figure b)
This last type of combinations is far more scanty, becaus of the fact that even T-values are ' notin the game' .
|
|


|
different levels of cristalline figures occur besides and within each other.
The U/D-series generates different ' circuits of right/left/bendig of successive linesegments.
When the rotational axes are connected with the first line-segment drawn in,
all lower level circuits are enclosed within the highest level circuit. In the other case there occur also circuits besides the highest level circuit.
Thenumer and types of circuits can be graspecd by analysing the way the successeve intersectionpoint at the strat of a segment ar linking together ongroun of value enlargement becaus of shiftdistance. in the higest level circuit
|
II Examples
Hierarchy and redundancy
hierarchy
Every time a link is added to the continued fraction, another layer is added to
the figure complexity that was being generated.
|
 | q=2 |
 |
q1=2
q2=2
q3=2
q4=2
|
 | q1=2
q2=2
|
 | q1=2
q2=2
q3=2
|
hierarchy
Succession of of even and oneven q-values in the series of q-values
Relation between grid in the outline and overall contour of the outline

|
 | |
 |

|
 | |
 |
 | |
 |
|